TEMAS I PERIODO-FÍSICA.
1. Factorizacion
2. Notación científica
3. Gráficas
4.Vectores
4.1.Suma y resta
5.Modulo
TRINOMIO CUADRADO PERFECTO:
FACTOR COMÚN:
DIFERENCIA DE CUADRADOS:
Y=MX ( LA RECTA PASA POR EL ORIGEN)
La Y son las abscisas,la X son las ordenadas y la M es la pendiente.
CASO 2.
VECTORES.
MAGNITUDES VECTORIALES: Es una magnitud física que esta expresada mediante un valor numérico o magnitud llamado modulo y una orientación en el espacio,esta se realiza con unas coordenadas cartesianas que son (X,Y,Z).
EJEMPLO:
FORMULA:

SEGÚN SUS LADOS:
SEGÚN SUS ÁNGULOS:



TIPOS DE FUNCIONES.

SOBREYECTIVA:

BIYECTIVA:
FUNCIONES POLINOMICAS.
PASO 1:
HALLAR PUNTOS DE CORTE.
PASOS FUNCIÓN RACIONAL: y:5/x-1
PASO 1:
HALLAR PUNTOS DE CORTE.
FACTORIZACION.
Es el proceso de presentar una expresión matemática o un numero en forma de multiplicación.Cabe recordar que los factores son elementos de la multiplicación y el resultado se conoce como producto.
CASOS DE FACTORIZACION:
TRINOMIO CUADRADO PERFECTO:
Se llama trinomio cuadrado perfecto al trinomio (tres términos) ya que dos de sus términos son cuadrados perfectos y el otro término es el doble producto de las bases de esos cuadrados.
FACTOR COMÚN:
Consiste en identificar un factor que se repita en todos los términos del polinomio dado.Este método esta basado en la propiedad distributiva de los números reales pero de forma contraria.
DIFERENCIA DE CUADRADOS:
Se le llama así al binomio (2) conformado por dos términos los cuales se le puede sacar raíz cuadrada exacta.
NOTACIÓN CIENTÍFICA.
Es un modo de escribir los números de forma abreviada,facilitando el trabajo con cantidades grandes o muy pequeñas.Es expresar cualquier cantidad multiplicada por una potencia de base 10.
La coma siempre se desplazara hacia la derecha cuando es negativo y hacia la izquierda cuando es positivo.
GRÁFICAS.
Esta conformado por X y Y.
Funciones lineales:
Es una función polinomica,es decir, una función que en el plano cartesiano se representa en una linea recta.
Y=MX ( LA RECTA PASA POR EL ORIGEN)
La Y son las abscisas,la X son las ordenadas y la M es la pendiente.
CASO 2.
Es cuando Y=MX+B no pasa por el origen y se forma por dos semirrectas.
La pendiente M es una inclinación y Y es función de X.
Las abscisas son Y y las ordenadas son X.
PENDIENTE.
⬇
VECTORES.
Son elementos que permiten representar magnitudes físicas mediante un valor numérico llamado modulo y una orientación.(Siempre parte desde el origen que es el 0)
CARACTERÍSTICAS:
ORIGEN:Todo vector debe partir de un punto para alcanzar el objetivo que se plantee.
Se debe tener en cuenta la magnitud y la dirección.
MAGNITUDES VECTORIALES: Es una magnitud física que esta expresada mediante un valor numérico o magnitud llamado modulo y una orientación en el espacio,esta se realiza con unas coordenadas cartesianas que son (X,Y,Z).
EJEMPLO:
LA ACELERACIÓN.
LA VELOCIDAD.
CAMPO ELÉCTRICO.
EL PESO.
CAMPO ELÉCTRICO.
EL PESO.
SUMA Y RESTA DE VECTORES.
Se realiza sumando o restando cada uno de su componentes dando como resultado otro vector.
FORMULAS:
SUMA: A+B= (X1; Y1)+(X2;Y2)=(X1+X2;Y1+Y2).
RESTA: A-B= (X1;Y1)-(X2;Y2)=(X1-X2;Y1-Y2).
MODULO.
Es lo que mide un vector,representa su longitud debido a que se trata a la hipotenusa de un triangulo rectángulo.
FORMULA:

TEMAS II PERIODO-TRIGONOMÉTRIA
1. Triángulos.
1.1. Según sus lados.
1.2. Según sus ángulos.
1.3. clasificación.
1.4. Ángulos.
2.Cuadrado de una suma.
3.Funciones.
4.Tipos de funciones Y pasos.
4.1. Polinomicas.
4.2. Racionales.
4.3. Radicales.
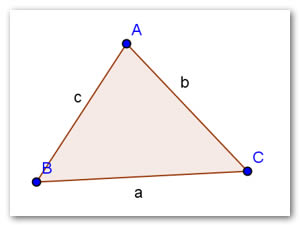
TRIÁNGULOS.
Un triangulo es un polígono que resulta unirse con 3 lineas rectas .
Todo triangulo tiene tres lados que son A , B y C. Tres vértices A , B y C. Y tres ángulos internos A , B y C.
SEGÚN SUS LADOS:
Hay tres tipos de triángulos según sus lados y son:
- TRIANGULO ISÓSCELES:
Este triangulo tiene 2 lados iguales y uno diferente.
- TRIANGULO ESCALENO:
Este tiene sus tres lados diferentes y sus ángulos también
- TRIANGULO EQUILATERO.
Este triangulo tiene todos sus lados y ángulos iguales.
SEGÚN SUS ÁNGULOS:
- TRIANGULO OBTUSÁNGULO:
Es aquel que tiene un angulo obtuso,es decir,que mide mas de 90° .

- TRIANGULO RECTÁNGULO:
Es aquel que posee un angulo recto,es decir, un angulo de 90° .
- TRIANGULO ACUTÁNGULO:
Es aquel que tiene tres lados agudos quiere decir que sus lados miden menos de 90 ⁰.

CUADRADO DE UNA SUMA.
Consiste en sumar dos cuadrados del primer miembro mas el doble del producto de ambos.
Generalizando con A y B que son cualquier numero.
FORMULA:
A+B2 =A2 +2AB+B2
CUADRADO DE UNA DIFERENCIA.
Se debe colocar el primer termino elevado al cuadrado menos el doble del producto del primer termino,mas el cuadrado de segundo termino.
FORMULA:
(a - b)2 = A2 - 2ab + B2
FUNCIONES.
Es una relación entre un conjunto A llamado dominio o conjunto de partida (DOMF) y B llamado codominio o conjunto de llegada (DOMF).
El recorrido o rango de una función es el conjunto de imágenes F(X) subconjunto del codominio de la función y se simboliza como RANF.
PARA SABER CUANDO ES FUNCIÓN SE DEBE TENER EN CUENTA QUE:
- Todo elemento del conjunto de partida tiene imagen.
- La imagen de cada elemento X es única.
- Y puede tener una,ninguna o varias preimagenes.
FORMAS DE REPRESENTACIÓN:
DIAGRAMA SAGITAL:

TRABLA DE VALORES:
TIPOS DE FUNCIONES.
INYECTIVA:
También llamada función 1 a 1 , es decir, relaciona cada elemento del conjunto de partida con un elemento del conjunto de llegada.

SOBREYECTIVA:
Cuando todo el codominio es el rango.
BIYECTIVA:
Cuando es biyectiva y sobreyectiva al mismo tiempo.
FUNCIONES POLINOMICAS.
- Y=C Función constante
- Y=X Función de identidad
- Y= Mx Función lineal
- Y=Mx+b Función a fin
- Y=X al cuadrado Función cuadrática
- Y=X al cubo Función cubica
PASOS FUNCIÓN POLINOMICA: y=3x
PASO 1:
HALLAR PUNTOS DE CORTE.
PASO 2:
HACER LA TABLA DE VALORES.
PASO 3:
TRAFICAR EN EL PLANO LO DE LA TABLA DE VALORES.
PASOS FUNCIÓN RACIONAL: y:5/x-1
PASO 1:
HALLAR PUNTOS DE CORTE.
PASO 2:
CALCULO DE LA FUNCIÓN INDETERMINADA.
CALCULO DE LA FUNCIÓN INDETERMINADA.
PASO 3:
CALCULO DEL DOMINIO.
CALCULO DEL DOMINIO.
PASO 4:
CREAR TABLA DE VALORES.
PASO 5:
GRAFICAR EN EL PANO CARTESIANO.
CREAR TABLA DE VALORES.
PASO 5:
GRAFICAR EN EL PANO CARTESIANO.
PASO 6:
CALCULAR EL RANGO.